The diagram shows the Maxwell-Boltzmann curve for the uncatalyzed reaction.

Draw a distribution curve at a lower temperature (T₂) and show on the diagram how the addition of a catalyst enables the reaction to take place more rapidly than at T₁.

The hydrogen peroxide could cause further oxidation of the methanol. Suggest a possible oxidation product.

Determine the overall equation for the production of methanol.

8.00 g of methane is completely converted to methanol. Calculate, to three significant figures, the final volume of hydrogen at STP, in dm³. Use sections 2 and 6 of the data booklet.

Determine the enthalpy change, ΔH, in kJ. Use section 11 of the data booklet.

Bond enthalpy of CO = 1077 kJ mol⁻¹.

State one reason why you would expect the value of ΔH calculated from the $∆H_f^{\mathrm{⦵}}$ values, given in section 12 of data booklet, to differ from your answer to (d)(i).

State the expression for K_c for this stage of the reaction.

State and explain the effect of increasing temperature on the value of K_c.

The equilibrium constant, K_c, has a value of 1.01 at 298 K.

Calculate ΔG^⦵, in kJ mol^–1, for this reaction. Use sections 1 and 2 of the data booklet.

Calculate a value for the entropy change, ΔS^⦵, in J K^–1 mol^–1 at 298 K. Use your answers to (e)(i) and section 1 of the data booklet.

If you did not get answers to (e)(i) use –1 kJ, but this is not the correct answer.

Justify the sign of ΔS with reference to the equation.

Predict, giving a reason, how a change in temperature from 298 K to 273 K would affect the spontaneity of the reaction.

curve higher AND to left of T₁ ✔

new/catalysed E_a marked AND to the left of E_a of curve T₁ ✔

Do not penalize curve missing a label, not passing exactly through the origin, or crossing x-axis after E_a.
Do not award M1 if curve drawn shows significantly more/less molecules/greater/smaller area under curve than curve 1.
Accept E_a drawn to T₁ instead of curve drawn as long as to left of marked E_a.

methanoic acid/HCOOH/CHOOH
OR
methanal/HCHO ✔

Accept “carbon dioxide/CO₂”.

CH₄(g) + H₂O(g) $\rightleftharpoons$ CH₃OH(l) + H₂(g) ✔

Accept arrow instead of equilibrium sign.

amount of methane = « $\frac{8.00 \mathrm{g}}{16.05 \mathrm{g} {\mathrm{mol}}^{-1}}$ = » 0.498 «mol» ✔

amount of hydrogen = amount of methane / 0.498 «mol» ✔

volume of hydrogen = «0.498 mol × 22.7 dm³mol⁻¹ = » 11.3 «dm³» ✔

Award [3] for final correct answer.
Award [2 max] for 11.4 «dm³ due to rounding of mass to 16/moles to 0.5. »

Σbonds broken = 4 × 414 «kJ» + 2 × 463 «kJ» / 2582 «kJ» ✔

Σbonds formed = 1077 «kJ» + 3 × 436 «kJ» / 2385 «kJ» ✔

ΔH «= Σbonds broken − Σbonds formed =( 2582 kJ − 2385 kJ)» = «+»197«kJ» ✔

Award [3] for final correct answer.
Award [2 Max] for final answer of −197 «kJ»

bond energies are average values «not specific to the compound» ✔

$K_{\mathit{c}}=\frac{\left[\mathrm{CO}\right]{\left[{\mathrm{H}}_2\right]}^3}{\left[{\mathrm{CH}}_4\right]\left[{\mathrm{H}}_2\mathrm{O}\right]}$ ✔

K_c increases AND «forward» reaction endothermic ✔

«ΔG^⦵ = − RT lnK_c»
ΔG^⦵ = − 8.31 «J K⁻¹ mol⁻¹» × 298 «K» × ln (1.01) / −24.6 «J mol⁻¹» ✔

= −0.0246 «kJ mol^–1» ✔

Award [2] for correct final answer.

Award [1 max] for +0.0246 «kJ mol^–1».

«ΔG^⦵ = ΔH^⦵ − TΔS^⦵»

ΔG^⦵ = −129 «kJ mol^–1» − (298 «K» × ΔS) = −0.0246 «kJ mol^–1» ✔

ΔS^⦵ = « $\frac{\left(129 \mathrm{kJ} {\mathrm{mol}}^{-1}+0.0246 \mathrm{kJ} {\mathrm{mol}}^{-1}\right)\times {10}^3}{298 \mathrm{K}}$ = » −433 «J K^–1 mol^–1» ✔

Award [2] for correct final answer.

Award [1 max] for “−0.433 «kJ K^–1mol^–1»”.

Award [1 max] for “433” or “+433” «J K^–1 mol^–1».

Award [2] for −430 «J K^–1 mol^–1» (result from given values).

«negative as» product is liquid and reactants gases
OR
fewer moles of gas in product ✔

reaction «more» spontaneous/ΔG negative/less positive AND effect of negative entropy decreases/TΔS increases/is less negative/more positive
OR
reaction «more» spontaneous/ΔG negative/less positive AND reaction exothermic «so K_c increases » ✔

Award mark if correct calculation shown.

Suggest how the extent of decomposition could be measured.

Plot the missing point on the graph and draw the best-fit line.

Outline why increasing the concentration of N₂O₅ increases the rate of reaction.

Write the rate expression for this reaction.

Calculate the value of the rate constant, k, giving its units.

use colorimeter
OR
change in colour
OR
change in volume
OR
change in pressure ✔

Accept suitable instruments, e.g. pressure probe/oxygen sensor.

point correct ✔

straight line passing close to all points AND through origin ✔

Accept free hand drawn line as long as attempt to be linear and meets criteria for M2.

greater frequency of collisions «as concentration increases»
OR
more collisions per unit time «as concentration increases» ✔

Accept “rate/chance/probability/likelihood” instead of “frequency”.

Do not accept just “more collisions”.

rate = k[N₂O₅] ✔

k = $\frac{∆\mathrm{rate}}{∆\left[{\mathrm{N}}_2{\mathrm{O}}_5\right]}$ ✔

«k = $\frac{0.75\times {10}^{-3}«\mathrm{mol} {\mathrm{dm}}^{-3} {\min }^{-1}»}{25\times {10}^{-3}«\mathrm{mol} {\mathrm{dm}}^{-3}»}$= » 0.030 «min^–1» ✔

min^–1 ✔

M1 can be awarded from correct M2 if not explicitly stated.

Accept k = gradient.

Accept values in the range 0.028–0.032.

Award [3] for correct final answer.

Explain why, as the reaction proceeds, the pressure increases by the amount shown.

Outline, in terms of collision theory, how a decrease in pressure would affect the rate of reaction.

Deduce how the rate of reaction at t = 2 would compare to the initial rate.

It has been suggested that the reaction occurs as a two-step process:

Step 1: N₂O (g) → N₂ (g) + O (g)

Step 2: N₂O (g) + O (g) → N₂ (g) + O₂ (g)

Explain how this could support the observed rate expression.

The experiment is repeated using the same amount of dinitrogen monoxide in the same apparatus, but at a lower temperature.

Sketch, on the axes in question 2, the graph that you would expect.

The experiment gave an error in the rate because the pressure gauge was inaccurate.

Outline whether repeating the experiment, using the same apparatus, and averaging the results would reduce the error.

The graph below shows the Maxwell–Boltzmann distribution of molecular energies at a particular temperature.

The rate at which dinitrogen monoxide decomposes is significantly increased by a metal oxide catalyst.

Annotate and use the graph to outline why a catalyst has this effect.

Determine the standard entropy change, in J K−1, for the decomposition of dinitrogen monoxide.

2N₂O (g) → 2N₂ (g) + O₂ (g)

Dinitrogen monoxide has a positive standard enthalpy of formation, ΔH_f^θ.

Deduce, giving reasons, whether altering the temperature would change the spontaneity of the decomposition reaction.

increase in the amount/number of moles/molecules «of gas»     [✔]

from 2 to 3/by 50 %     [✔]

«rate of reaction decreases»
concentration/number of molecules in a given volume decreases
OR
more space between molecules    [✔]

collision rate/frequency decreases
OR
fewer collisions per unit time     [✔]

Note: Do not accept just “larger space/volume” for M1.

half «of the initial rate»    [✔]

Note: Accept “lower/slower «than initial rate»”.

1 slower than 2
OR
1 rate determinant step/RDS    [✔]

1 is unimolecular/involves just one molecule so it must be first order
OR
if 1 faster/2 RDS, second order in N₂O
OR
if 1 faster/2 RDS, first order in O     [✔]

smaller initial gradient     [✔]

initial pressure is lower AND final pressure of gas lower «by similar factor»     [✔]

no AND it is a systematic error/not a random error

OR

no AND «a similar magnitude» error would occur every time     [✔]

catalysed and uncatalysed E_a marked on graph AND with the catalysed being at lower energy     [✔]

«for catalysed reaction» greater proportion of/more molecules have E ≥ E_a / E > E_a
OR
«for catalysed reaction» greater area under curve to the right of the E_a     [✔]

Note: Accept “more molecules have the activation energy”.

ΔS^θ = 2(S^θ(N₂)) + S^θ(O₂) – 2(S^θ(N₂O))
OR
ΔS^θ = 2 × 193 «J mol^-1 K^-1» + 205 «J mol^-1 K^-1» – 2 × 220 «J mol^-1 K^-1»     [✔]

«ΔS^θ = +»151 «J K^-1»     [✔]

Note: Award [2] for correct final answer.

exothermic decomposition
OR
ΔH_{(decomposition)} < 0    [✔]

TΔS^θ > ΔH^θ
OR
ΔG^θ «= ΔH^θ – TΔS^θ» < 0 «at all temperatures»     [✔]

reaction spontaneous at all temperatures    [✔]

Students were able in general to relate more moles of gas to increase in pressure.

Few students were able to relate the effect of reduced pressure at constant volume with a decrease in concentration of gas molecules and mostly did not even refer to this, but rather concentrated on lower rate of reaction and frequency of collisions. Many candidates lost a mark by failing to explain rate as collisions per unit time, frequency, etc.

Though the differential equation was considered to be misleading by teachers, most candidates attempted to answer this question, and more than half did so correctly, considering they had the graph to visualize the gradient.

Most students were able to identity step 1 as the RDS/slow but few mentioned unimolecularity or referred vaguely to NO₂ as the only reagent (which was obvious) and got only 1 mark.

Many students drew a lower initial gradient, but most did not reflect the effect of lower temperature on pressure at constant volume and started and finished the curve at the same pressure as the original one.

Almost all candidates identified the inaccurate pressure gauge as a systematic error, thus relating accuracy to this type of error.

The graph was generally well done, but in quite a few cases, candidates did not mention that increase of rate in the catalyzed reaction was due to E (particles) > E_a or did so too vaguely.

Candidates were able to calculate the ΔS of the reaction, though in some cases they failed to multiply by the number of moles.

Though the question asked for decomposition (in bold), most candidates ignored this and worked on the basis of a the ΔH of formation. However, many did write a sound explanation for that situation. On the other hand, in quite a number of cases, they did not state the sign of the ΔH (probably taking it for granted) nor explicitly relate ΔG and spontaneity, which left the examiner with no possibility of evaluating their reasoning.

Suggest how the change of iodine concentration could be followed.

A student produced these results with $[{\text{H}}^{+}]=0.15\text{ mol}\text{d}{\text{m}}^{-3}$. Propanone and acid were in excess and iodine was the limiting reagent. Determine the relative rate of reaction when $[{\text{H}}^{+}]=0.15\text{ mol}\text{d}{\text{m}}^{-3}$.

The student then carried out the experiment at other acid concentrations with all other conditions remaining unchanged.

Determine the relationship between the rate of reaction and the concentration of acid and the order of reaction with respect to hydrogen ions.

When the concentration of iodine is varied, while keeping the concentrations of acid and propanone constant, the following graphs are obtained.

Deduce, giving your reason, the order of reaction with respect to iodine.

When the reaction is carried out in the absence of acid the following graph is obtained.

Discuss the shape of the graph between A and B.

use a colorimeter/monitor the change in colour

OR

take samples AND quench AND titrate «with thiosulfate»

Accept change in pH.

Accept change in conductivity.

Accept other suitable methods.

Method must imply “change”.

[1 mark]

best fit line

relative rate of reaction $=\ll \frac{-\mathrm{\Delta }y}{\mathrm{\Delta }x}=\frac{-(0.43-0.80)}{50}=\gg 0.0074/7.4\times {10}^{-3}$

Best fit line required for M1.

M2 is independent of M1.

Accept range from 0.0070 to 0.0080.

[2 marks]

Relationship:
rate of reaction is «directly» proportional to [H⁺]
OR
rate of reaction $\alpha$ [H⁺] 

Order of reaction with respect to [H⁺]:
first

Accept "doubling the concentration doubles the rate".

Do not accept “rate increases as concentration increases”.

[2 marks]

zero order

rate of reaction is the same for all concentrations of iodine

Accept “all graphs have same/similar gradient”.

[2 marks]

slow rate of reaction which gradually increases

as H⁺ ions are produced «to catalyse the reaction»
OR
reaction is autocatalytic

M1 should mention “rate of reaction”.

[2 marks]

Nitrogen monoxide reacts with oxygen gas to form nitrogen dioxide.

The following experimental data was obtained.

Deduce the partial order of reaction with respect to nitrogen monoxide and oxygen.

Nitrogen monoxide reacts with oxygen gas to form nitrogen dioxide.

Deduce, giving a reason, whether the following mechanism is possible.

$NO$: second ✔
$O_2$: first ✔

not possible AND «proposed» mechanism does not match experimental rate law
OR
not possible AND «proposed» mechanism shows zero/not first order with respect to oxygen ✔

Most candidates could correctly deduce the order of each reactant from rate experimental rate data.

60% of candidates could explain why the proposed reaction mechanism was inconsistent with the empirical data given.

Outline how a catalyst increases the rate of reaction.

Explain why an increase in temperature increases the rate of reaction.

Discuss, referring to intermolecular forces present, the relative volatility of propanone and propan-2-ol.

The diagram shows an unlabelled voltaic cell for the reaction

${\mathrm{Pb}}^{2+}\left(\mathrm{aq}\right)+\mathrm{Ni}\left(\mathrm{s}\right)\to {\mathrm{Ni}}^{2+}\left(\mathrm{aq}\right)+\mathrm{Pb}\left(\mathrm{s}\right)$

Label the diagram with the species in the equation.

Calculate the standard cell potential, in $\mathrm{V}$, for the cell at $298 \mathrm{K}$. Use section 24 of the data booklet

Calculate the standard free energy change, $∆{\mathrm{G}}^{⦵}$, in $\mathbf{kJ}$, for the cell using sections 1 and 2 of the data booklet.

Suggest a metal that could replace nickel in a new half-cell and reverse the electron flow. Use section 25 of the data booklet.

Describe the bonding in metals.

Nickel alloys are used in aircraft gas turbines. Suggest a physical property altered by the addition of another metal to nickel.

provides an alternative pathway/mechanism AND lower E_a ✔

Accept description of how catalyst lowers E_a (e.g. “reactants adsorb on surface «of catalyst»”, “reactant bonds weaken «when adsorbed»”).

more/greater proportion of molecules with E E_a ✔

greater frequency/probability/chance of collisions «between the molecules»
OR
more collision per unit of time/second ✔

hydrogen bonding/bonds «and dipole–dipole and London/dispersion forces are present in» propan-2-ol ✔

dipole–dipole «and London/dispersion are present in» propanone ✔

propan-2-ol less volatile AND hydrogen bonding/bonds stronger «than dipole–dipole »
OR
propan-2-ol less volatile AND «sum of all» intermolecular forces stronger ✔

$«-0.13 \mathrm{V}-(-0.26 \mathrm{V})=+»0.13«\mathrm{V}»$ ✔

$«{\mathrm{\Delta G}}^{\mathrm{\Theta }}=-{\mathrm{nFE}}^{\mathrm{\Theta }}=-2\times 96 500\times \frac{0.13}{1000}=»-25 «\mathrm{k} \mathrm{J}»$ ✔

$\mathrm{Bi}/\mathrm{Cu}/\mathrm{Ag}/\mathrm{Pd}/\mathrm{Hg}/\mathrm{Pt}/\mathrm{Au}$ ✔

Accept $Sb$ OR $As$.

electrostatic attraction ✔

between «a lattice of» metal/positive ions/cations AND «a sea of» delocalized electrons ✔

Accept “mobile/free electrons”.

Any of:

malleability/hardness
OR
«tensile» strength/ductility
OR
density
OR
thermal/electrical conductivity
OR
melting point
OR
thermal expansion ✔

Do not accept corrosion/reactivity or any chemical property.

Accept other specific physical properties.

Although fairly well done some candidates did not mention that providing an alternate pathway to the reaction was how the activation energy was lowered and hence did not gain the mark.

Almost all candidates earned at least 1 mark for the effect of temperature on rate. Some missed increase in collision frequency, others the idea that more particles reached the required activation energy.

The average mark was 1.9/3. Almost all candidates could recognize hydrogen bonding in alcohol but many missed the dipole-dipole attraction in propanone. There was also some confusion on the term volatility, with some thinking stronger IMF meant higher volatility.

A surprising number of No Response for a question where candidates simply had to label a diagram with the species in the equation. Some candidates had the idea but did not use the species for electrolytic cell, e.g., Pb(SO₄) instead of Pb²⁺(aq).

80% of candidates could correctly calculate a cell potential by using a reduction table and a balanced redox reaction. 

This was similar to 2f(ii) where many could apply the formula for Gibbs free energy change, ΔG^ө, correctly however some did not get the units correct.

80% could correctly pick a metal to reverse the electron flow, however some candidates thought a more reactive, rather than a less reactive metal than nickel would reverse the electron flow.

Most candidates were aware that metallic bonding involved a "sea of electrons", but were unsure about surrounding what and could not identify that it was electrostatic attraction holding the metal together.

Almost all candidates could correctly identify a physical property of a metal which might be altered when alloying.

Determine the limiting reactant showing your working.

The mass of copper obtained experimentally was 0.872 g. Calculate the percentage yield of copper.

The reaction was carried out in a calorimeter. The maximum temperature rise of the solution was 7.5 °C.

Calculate the enthalpy change, ΔH, of the reaction, in kJ, assuming that all the heat released was absorbed by the solution. Use sections 1 and 2 of the data booklet.

State another assumption you made in (b)(i).

The only significant uncertainty is in the temperature measurement.

Determine the absolute uncertainty in the calculated value of ΔH if the uncertainty in the temperature rise was ±0.2 °C.

Sketch a graph of the concentration of iron(II) sulfate, FeSO₄, against time as the reaction proceeds.

Outline how the initial rate of reaction can be determined from the graph in part (c)(i).

Explain, using the collision theory, why replacing the iron powder with a piece of iron of the same mass slows down the rate of the reaction.

A student electrolyzed aqueous iron(II) sulfate, FeSO₄ (aq), using platinum electrodes. State half-equations for the reactions at the electrodes, using section 24 of the data booklet.

n_CuSO4 «= 0.0800 dm³ × 0.200 mol dm^–3» = 0.0160 mol AND

n_Fe «$\frac{3.26\text{g}}{55.85\text{g}\text{mo}{\text{l}}^{-1}}$» = 0.0584 mol ✔

CuSO₄ is the limiting reactant ✔

Do not award M2 if mole calculation is not shown.

ALTERNATIVE 1:
«0.0160 mol × 63.55 g mol^–1 =» 1.02 «g»  ✔

«$\frac{0.872\text{g}}{1.02\text{g}}\times 100=$» 85.5 «%»  ✔

ALTERNATIVE 2:
«$\frac{0.872\text{g}}{63.55\text{g}\text{mo}{\text{l}}^{--1}}=$» 0.0137 «mol»  ✔

«$\frac{0.0137\text{mol}}{0.0160\text{mol}}\times 100=$» 85.6 «%»  ✔

Accept answers in the range 85–86 %.

Award [2] for correct final answer.

ALTERNATIVE 1:

q = «80.0 g × 4.18 J g^–1 K^–1 × 7.5 K =» 2.5 × 10³ «J»/2.5 «kJ» ✔

«per mol of CuSO₄ = $\frac{-2.5\text{kJ}}{0.0160\text{mol}}=-1.6\times {10}^2$ kJ mol^–1»

«for the reaction» ΔH = –1.6 × 10² «kJ» ✔

ALTERNATIVE 2:

q = «80.0 g × 4.18 J g^–1 K^–1 × 7.5 K =» 2.5 × 10³ «J»/2.5 «kJ» ✔

«n_Cu = $\frac{0.872}{63.55}$ = 0.0137 mol»

«per mol of CuSO₄ = $\frac{-2.5\text{kJ}}{0.0137\text{mol}}=-1.8\times {10}^2$ kJ mol^–1»

«for the reaction» ΔH = –1.8 × 10² «kJ» ✔

Award [2] for correct final answer.

density «of solution» is 1.00 g cm⁻³

OR

specific heat capacity «of solution» is 4.18 J g⁻¹ K⁻¹/that of «pure» water

OR

reaction goes to completion

OR

iron/CuSO₄ does not react with other substances ✔

The mark for “reaction goes to completion” can only be awarded if 0.0160 mol was used in part (b)(i).

Do not accept “heat loss”.

ALTERNATIVE 1:

«$0.2{}^{\circ }\text{C}\times \frac{100}{7.5{}^{\circ }\text{C}}=$» 3 %/0.03 ✔

«0.03 × 160 kJ» = «±» 5 «kJ» ✔

ALTERNATIVE 2:

«$0.2{}^{\circ }\text{C}\times \frac{100}{7.5{}^{\circ }\text{C}}=$» 3 %/0.03 ✔

«0.03 × 180 kJ» = «±» 5 «kJ» ✔

Accept values in the range 4.1–5.5 «kJ».

Award [2] for correct final answer.

initial concentration is zero AND concentration increases with time ✔

decreasing gradient as reaction proceeds ✔

«draw a» tangent to the curve at time = 0 ✔

«rate equals» gradient/slope «of the tangent» ✔

Accept suitable diagram.

piece has smaller surface area ✔

lower frequency of collisions

OR

fewer collisions per second/unit time ✔

Accept “chance/probability” instead of “frequency”.

Do not accept just “fewer collisions”.

Anode (positive electrode):

2H₂O (l) → O₂ (g) + 4H⁺ (aq) + 4e^– ✔

Cathode (negative electrode):

2H₂O (l) + 2e^– → H₂ (g) + 2OH^– (aq)
OR
2H⁺ (aq) + 2e^– → H₂ (g) ✔

Accept “4OH^– (aq) → O₂ (g) + 2H₂O (l)  + 4e^–” OR “Fe²⁺ (aq) → Fe³⁺ (aq) + e^–” for M1.

Accept “Fe²⁺ (aq) + 2e^– → Fe (s)” OR “SO₄^2- (aq) 4H⁺ (aq) + 2e^– → 2H₂SO₃(aq) + H₂O (l)”
for M2.

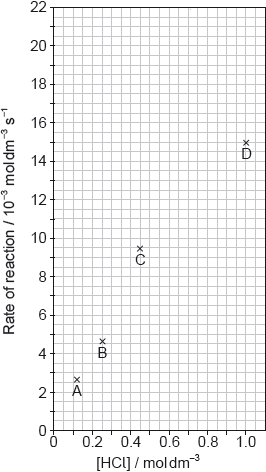
Outline two ways in which the progress of the reaction can be monitored. No practical details are required.

Suggest why point D is so far out of line assuming human error is not the cause.

Draw the best fit line for the reaction excluding point D.

Suggest the relationship that points A, B and C show between the concentration of the acid and the rate of reaction.

Deduce the rate expression for the reaction.

Calculate the rate constant of the reaction, stating its units.

Predict from your line of best fit the rate of reaction when the concentration of HCl is 1.00 mol dm⁻³.

Describe how the activation energy of this reaction could be determined.

Any two of:

loss of mass «of reaction mixture/CO₂»

«increase in» volume of gas produced

change of conductivity

change of pH

change in temperature

Do not accept “disappearance of calcium carbonate”.

Do not accept “gas bubbles”.

Do not accept “colour change” or “indicator”.

[2 marks]

reaction is fast at high concentration AND may be difficult to measure accurately

OR

so many bubbles of CO₂ produced that inhibit contact of HCl(aq) with CaCO₃(s)

OR

insufficient change in conductivity/pH at high concentrations

OR

calcium carbonate has been used up/is limiting reagent/ there is not enough calcium carbonate «to react with the high concentration of HCl»

OR

HCl is in excess

OR

so many bubbles of CO₂ produced that inhibit contact of HCl(aq) with CaCO₃(s)

[1 mark]

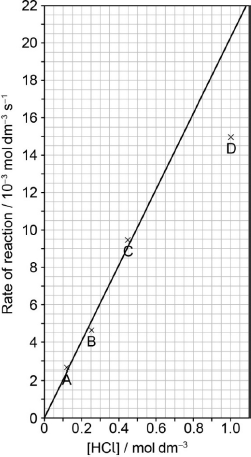
straight line going through the origin AND as close to A, B, C as is reasonably possible

[1 mark]

«directly» proportional

Accept “first order” or “linear”.

Do not accept “rate increases as concentration increases” or “positive correlation”.

[1 mark]

rate = k [H⁺]

Accept “rate = k [HCl]”.

[1 mark]

0.02

s^–1

[2 marks]

20.5 $\times$ 10^–3 «mol dm^–3 s^–1»

Accept any answer in the range 19.5–21.5.

[1 mark]

ALTERNATIVE 1:

carry out reaction at several temperatures

plot $\frac{1}{\text{T}}$ against log rate constant

E_a = – gradient $\times$ R

ALTERNATIVE 2:

carry out reaction at two temperatures

determine two rate constants

OR

determine the temperature coefficient of the rate

use the formula  $\ln \frac{k_1}{k_2}=\frac{E_{\text{a}}}{R}\left(\frac{1}{T_2}-\frac{1}{T_1}\right)$

Accept “gradient = $\frac{-E_{\text{a}}}{R}$” for M3.

Award both M2 and M3 for the formula  $\text{ln}\frac{rat{e}_1}{rat{e}_2}=\frac{E_{\text{a}}}{R}\left(\frac{1}{T_2}-\frac{1}{T_1}\right)$.

Accept any variation of the formula, such as $\frac{rat{e}_1}{rat{e}_2}=e^{-\frac{E_{\text{a}}}{R}\left(\frac{1}{T_1}-\frac{1}{T_2}\right)}$.

[3 marks]

Calcium carbonate is heated to produce calcium oxide, CaO.

CaCO₃(s) → CaO (s) + CO₂(g)

Calculate the volume of carbon dioxide produced at STP when 555 g of calcium carbonate decomposes. Use sections 2 and 6 of the data booklet.

Calculate the enthalpy change of reaction, ΔH, in kJ, for the decomposition of calcium carbonate.

Calculate the change in entropy, ΔS, in J K⁻¹, for the decomposition of calcium carbonate.

Determine the temperature, in K, at which the decomposition of calcium carbonate becomes spontaneous, using b(i), b(ii) and section 1 of the data booklet.

(If you do not have answers for b(i) and b(ii), use ΔH = 190 kJ and ΔS = 180 J K⁻¹, but these are not the correct answers.)

Sketch an energy profile for the decomposition of calcium carbonate based on your answer to b(i), labelling the axes and activation energy, E_a.

State how adding a catalyst to the reaction would impact the enthalpy change of reaction, ΔH, and the activation energy, E_a.

Write the equation for the reaction of Ca(OH)₂(aq) with hydrochloric acid, HCl (aq).

Determine the volume, in dm³, of 0.015 mol dm⁻³ calcium hydroxide solution needed to neutralize 35.0 cm³ of 0.025 mol dm⁻³ HCl (aq).

Saturated calcium hydroxide solution is used to test for carbon dioxide. Calculate the pH of a 2.33 × 10⁻²mol dm⁻³ solution of calcium hydroxide, a strong base.

Determine the mass, in g, of CaCO₃(s) produced by reacting 2.41 dm³ of 2.33 × 10⁻² mol dm⁻³ of Ca(OH)₂ (aq) with 0.750 dm³ of CO₂ (g) at STP.

2.85 g of CaCO₃ was collected in the experiment in d(i). Calculate the percentage yield of CaCO₃.

(If you did not obtain an answer to d(i), use 4.00 g, but this is not the correct value.)

Outline how one calcium compound in the lime cycle can reduce a problem caused by acid deposition.

«n_CaCO3 = $\frac{555 \mathrm{g}}{11.09 \mathrm{g} {\mathrm{mol}}^{-1}}$=» 5.55 «mol» ✓

«V = 5.55 mol × 22.7 dm³ mol⁻¹ =» 126 «dm³» ✓

Award [2] for correct final answer.

Accept method using pV = nRT to obtain the volume with p as either 100 kPa (126 dm³) or 101.3 kPa (125 dm³).

Do not penalize use of 22.4 dm³ mol^–1 to obtain the volume (124 dm³).

«ΔH =» (−635 «kJ» – 393.5 «kJ») – (−1207 «kJ») ✓

«ΔH = + » 179 «kJ» ✓

Award [2] for correct final answer.

Award [1 max] for −179 kJ.

Ignore an extra step to determine total enthalpy change in kJ: 179 kJ mol^-1 x 5.55 mol = 993 kJ.

Award [2] for an answer in the range 990 - 993« kJ».

«ΔS = (40 J K⁻¹ + 214 J K⁻¹) − (93 J K⁻¹) =» 161 «J K⁻¹» ✓

Ignore an extra step to determine total entropy change in JK^–1: 161 J mol^–1K^–1 x 5.55 mol = 894 «J mol^–1K^–1»

Award [1] for 894 «J mol^–1K^–1».

«spontaneous» if ΔG = ΔH − TΔS < 0
OR
ΔH < TΔS ✓

«T >$\frac{179 \mathrm{kJ}}{0.16 \mathrm{kJ} {\mathrm{K}}^{-1}}$=» 1112 «K» ✓

Award [2] for correct final answer.

Accept “1056 K” if both of the incorrect values are used to solve the problem.

Do not award M2 for any negative T value.

endothermic sketch ✓

x-axis labelled “extent of reaction/progress of reaction/reaction coordinate/reaction pathway” AND y-axis labelled “potential energy/energy/enthalpy✓

activation energy/E_a ✓

Do not accept “time” for x-axis.

ΔH same AND lower E_a ✓

Ca(OH)₂(aq) + 2HCl (aq) → 2H₂O (l) + CaCl₂(aq) ✓

«n_HCl = 0.0350 dm³ × 0.025 mol dm⁻³ =» 0.00088 «mol»

OR
n_Ca(OH)2 = $\frac{1}{2}$ n_HCl/0.00044 «mol» ✓

«V = $\frac{{\displaystyle \frac{1}{2}\times 0.00088 \mathrm{mol}}}{0.015 \mathrm{mol} {\mathrm{dm}}^{-3}}$ =» 0.029 «dm³» ✓

Award [2] for correct final answer.

Award [1 max] for 0.058 «dm³».

Alternative 1:

[OH⁻] = « 2 × 2.33 × 10⁻²mol dm⁻³ =» 0.0466 «mol dm⁻³» ✓

«[H⁺] = $\frac{1.00\times {10}^{-14}}{0.0466}$ = 2.15 × 10⁻¹³mol dm⁻³»

pH = « −log (2.15 × 10−13) =» 12.668 ✓

Alternative 2:

[OH⁻] =« 2 × 2.33 × 10⁻² mol dm⁻³ =» 0.0466 «mol dm⁻³» ✓

«pOH = −log (0.0466) = 1.332»

pH = «14.000 – pOH = 14.000 – 1.332 =» 12.668 ✓

Award [2] for correct final answer.

Award [1 max] for pH =12.367.

«n_Ca(OH)2 = 2.41 dm³ × 2.33 × 10⁻²mol dm⁻³ =» 0.0562 «mol» AND

«n_CO2 =$\frac{0.750 {\mathrm{dm}}^3}{22.7 \mathrm{mol} {\mathrm{dm}}^{-3}}$=» 0.0330 «mol» ✓

«CO₂ is the limiting reactant»

«m_CaCO3 = 0.0330 mol × 100.09 g mol⁻¹ =» 3.30 «g» ✓

Only award ECF for M2 if limiting reagent is used.

Accept answers in the range 3.30 - 3.35 «g».

«$\frac{2.85}{3.30}$ × 100 =» 86.4 «%» ✓

Accept answers in the range 86.1-86.4 «%».

Accept “71.3 %” for using the incorrect given value of 4.00 g.

«add» Ca(OH)₂/CaCO₃/CaO AND to «acidic» water/river/lake/soil
OR
«use» Ca(OH)₂/CaCO₃/CaO in scrubbers «to prevent release of acidic pollution» ✓

Accept any correct name for any of the calcium compounds listed.

Deduce the order of reaction with respect to hydrogen.

Deduce the rate expression for the reaction.

Calculate the value of the rate constant stating its units.

State two conditions necessary for a successful collision between reactants.

State the equilibrium constant expression, K_c, for this reaction.

Calculate the entropy change of reaction, ΔS^⦵, in J K⁻¹ mol⁻¹.

Predict, giving a reason, how the value of the ΔS^⦵_reaction would be affected if ${\text{I}}_2$ (g) were used as a reactant.

Calculate the Gibbs free energy change, ΔG^⦵, in kJ mol⁻¹, for the reaction at 298 K. Use section 1 of the data booklet.

Calculate the equilibrium constant, K_c, for this reaction at 298 K. Use your answer to (d)(iii) and sections 1 and 2 of the data booklet.

(If you did not obtain an answer to (d)(iii) use a value of 2.0 kJ mol⁻¹, although this is not the correct answer).

first order ✔

Rate=k [H₂] [$\text{I}$₂]

$k=«\frac{1.2\times {10}^{-6} \mathrm{mol} {\mathrm{dm}}^{-3} {\mathrm{s}}^{-1}}{2.0\times {10}^{-3} \mathrm{mol} {\mathrm{dm}}^{-3}\times 3.0\times {10}^{-3} \mathrm{mol} {\mathrm{dm}}^{-3}}=»0.20$ ✔

mol^–1 dm³ s^–1 ✔

E ≥ E_a AND appropriate «collision» geometry/correct orientation ✔

$K_{\mathrm{c}}=\frac{{\left[\mathrm{HI}\right]}^2}{\left[{\mathrm{H}}_2\right]\left[{\mathrm{I}}_2\right]}$ ✔

«Δ${S^{⦵}}_{\text{reaction}}$ = 2 × 206.6 – (130.6 + 116.1) =» 166.5 «J K^–1 mol^–1» ✔

Δ${S^{⦵}}_{\text{reaction}}$ lower/less positive AND same number of moles of gas

OR

Δ${S^{⦵}}_{\text{reaction}}$ lower/less positive AND a solid has less entropy than a gas ✔

«ΔG^⦵ = 53.0 kJ mol^–1 – (298K × 0.1665 kJ K^–1 mol^–1) =» 3.4 «kJ mol^–1» ✔

«ln K_c= – (3.4 × 10³ J mol^–1 /8.31 J K^–1 mol^–1 × 298 K)» = –1.37 ✔

«K_c =» 0.25 ✔

Award [2] for “0.45” for the use of 2.0 kJ mol^–1 for ΔG^⦵.

4(a)(i)-(iii): Deduction of rate orders and rate expression were very well done overall, with occasional errors in the units of the rate constant, but clearly among the best answered questions.

Generally well answered by all but very weak candidates. Some teachers thought this should be a 2-mark question but actually the marks were generally missed when students mentioned both required conditions but failed to refer the necessary energy to E_a.

One of the best answered questions.

ΔS was well calculated in general except for some inverted calculations or failure to consider the ratios of the reactants.

Some candidates confused the entropy change in this situation with absolute entropy of a solid and gas, or having realised that entropy would decrease lacked clarity in their explanations and lost the mark.

4(d)(ii)-(d)(iv): marks were lost due to inconsistency of units throughout, i.e., not because answers were given in different units to those required, but because candidates failed to convert all data to the same unit for calculations.

State the name of Compound B, applying International Union of Pure and Applied Chemistry (IUPAC) rules.

Compound A and Compound B are both liquids at room temperature and pressure. Identify the strongest intermolecular force between molecules of Compound A.

State the number of $\text{σ}$ (sigma) and $\mathrm{\pi }$ (pi) bonds in Compound A.

Deduce the hybridization of the central carbon atom in Compound A.

Identify the isomer of Compound B that exists as optical isomers (enantiomers).

Draw the structural formula of the alkene required.

Explain why the reaction produces more (CH₃)₃COH than (CH₃)₂CHCH₂OH.

Deduce the structural formula of the repeating unit of the polymer formed from this alkene.

Deduce what would be observed when Compound B is warmed with acidified aqueous potassium dichromate (VI).

Identify the type of reaction.

Outline the requirements for a collision between reactants to yield products.

Explain the mechanism of the reaction using curly arrows to represent the movement of electron pairs.

The polarity of the carbon–halogen bond, C–X, facilitates attack by HO^–.

Outline, giving a reason, how the bond polarity changes going down group 17.

2-methylpropan-2-ol /2-methyl-2-propanol ✔

Accept methylpropan-2-ol/ methyl-2-propanol.

Do not accept 2-methylpropanol.

dipole-dipole ✔

Do not accept van der Waals’ forces.

$\text{σ}$: 9
AND
$\mathrm{\pi }$: 1 ✔

sp² ✔

butan-2-ol/CH₃CH(OH)C₂H₅ ✔

carbocation formed from (CH₃)₃COH is more stable / (CH₃)₃C⁺ is more stable than (CH₃)₂CHCH₂⁺ ✔

«because carbocation has» greater number of alkyl groups/lower charge on the atom/higher e^- density
OR
«greater number of alkyl groups» are more electron releasing
OR
«greater number of alkyl groups creates» greater inductive/+I effect ✔

Do not award any marks for simply quoting Markovnikov’s rule.

Do not penalize missing brackets or n.

Do not award mark if continuation bonds are not shown.

no change «in colour/appearance/solution» ✔

«nucleophilic» substitution
OR
SN2 ✔

Accept “hydrolysis”.

Accept SN1

energy/E ≥ activation energy/E_a ✔

correct orientation «of reacting particles»
OR
correct geometry «of reacting particles» ✔

curly arrow going from lone pair/negative charge on O in ^-OH to C ✔

curly arrow showing I leaving ✔

representation of transition state showing negative charge, square brackets and partial bonds ✔

Accept OH^- with or without the lone pair.

Do not allow curly arrows originating on H, rather than the -, in OH^-.

Accept curly arrows in the transition state.

Do not penalize if HO and I are not at 180°.

Do not award M3 if OH–C bond is represented.

Award [2 max] if S_N1 mechanism shown.

decreases/less polar AND electronegativity «of the halogen» decreases ✔

Accept “decreases” AND a correct comparison of the electronegativity of two halogens.

Accept “decreases” AND “attraction for valence electrons decreases”.

Naming the organic compound using IUPAC rules was generally done well.

Mediocre performance in stating the number of σ (sigma) and π (pi) bonds in propanone; the common answer was 3 σ and 1 π instead of 9 σ and 1 π, suggesting the three C-H σ bonds in each of the two methyl groups were ignored.

sp² hybridization of the central carbon atom in the ketone was very done well.

Mediocre performance; some identified 2-methylpropan-1-ol or -2-ol, instead butan-2-ol/CH₃CH(OH)C₂H₅ as the isomer that exists as an optical isomer.

Good performance; some had a H and CH₃ group on each C atom across double bond instead of having two H atoms on one C and two CH₃ groups on the other.

Poor performance, particularly in light of past feedback provided in similar questions since there was repeated reference simply to Markovnikov's rule, without any explanation.

Mediocre performance; deducing structural formula of repeating unit of the polymer was challenging in which continuation bonds were sometimes missing, or structure included a double bond or one of the CH₃ group was missing.

Mediocre performance; deducing whether the tertiary alcohol could be oxidized solicited mixed responses ranging from the correct one, namely no change (in colour, appearance or solution), to tertiary alcohol will be reduced, or oxidized, or colour will change will occur, and such.

Excellent performance on the type of reaction but with some incorrect answers such as alkane substitution, free radical substitution or electrophilic substitution.

Good performance. For the requirements for a collision between reactants to yield products, some suggested necessary, sufficient or enough energy or even enough activation energy instead of energy/E ≥ activation energy/E_a.

Mechanism for SN2 not done well. Often the negative charge on OH was missing, the curly arrow was not going from lone pair/negative charge on O in -OH to C, or the curly arrow showing I leaving placed incorrectly and specially the negative charge was missing in the transition state. Formation of a carbocation intermediate indicating SN1 mechanism could score a maximum of 2 marks.

Good performance on how the polarity of C-X bond changes going down group 17.

Outline, giving a reason, the effect of a catalyst on a reaction.

On the axes, sketch Maxwell–Boltzmann energy distribution curves for the reacting species at two temperatures T₁ and T₂, where T₂ > T₁.

Explain the effect of increasing temperature on the yield of SO₃.

Draw the Lewis structure of SO₃.

Explain the electron domain geometry of SO₃.

State the product formed from the reaction of SO₃ with water.

State the meaning of a strong Brønsted–Lowry acid.

increases rate AND lower E_a ✔

provides alternative pathway «with lower E_a»
OR
more/larger fraction of molecules have the «lower» E_a ✔

Accept description of how catalyst lowers E_a for M2 (e.g. “reactants adsorb on surface «of catalyst»”, “reactant bonds weaken «when adsorbed»”, “helps favorable orientation of molecules”).

both axes correctly labelled ✔

peak of T₂ curve lower AND to the right of T₁ curve ✔

lines begin at origin AND correct shape of curves AND T₂ must finish above T₁ ✔

Accept “probability «density» / number of particles / N / fraction” on y-axis.

Accept “kinetic E/KE/E_k” but not just “Energy/E” on x-axis.

decrease AND equilibrium shifts left / favours reverse reaction ✔

«forward reaction is» exothermic / ΔH is negative ✔

✔

Note:

Accept any of the above structures as formal charge is not being assessed.

three electron domains «attached to the central atom» ✔

repel/as far away as possible /120° «apart» ✔

sulfuric acid/H₂SO₄ ✔

Accept “disulfuric acid/H₂S₂O₇”.

fully ionizes/dissociates ✔

proton/H⁺ «donor »✔

Overall well answered though some answers were directed to explain the specific example rather than the simple and standard definition of the effect of a catalyst.

Few got the 3 marks for this standard question (average mark 1.7), the most common error being incomplete/incorrect labelling of axes, curves beginning above 0 on y-axis or inverted curves.

Many candidates got one mark at least, sometimes failing to state the effect on the production of SO₃ though they knew this quite obviously. This failure to read the question properly also resulted in an incorrect prediction based exclusively on kinetics instead of using the information provided to guide their answers.

Drawing the Lewis structure of SO₃ proved to be challenging, with lots of incorrect shapes, lone pair on S, etc.; accepting all resonant structures allowed many candidates to get the mark which was fair considering no formal charge estimation was required.

Most were focussed on the shape itself instead of explaining what led them to suggest that shape; number of electron domains allowed most candidates to get one mark and eventually a mention of bond angles resulted in only 35% getting both marks. In general, students were not able to provide clear explanations for the shape (not a language issue) but rather were happy to state the molecular geometry which they knew, but wasn't what was actually required for the mark.

6(d)(i)-(ii): These simple questions could be expected to be answered by all HL candidates. However 20% of the candidates suggested hydroxides or hydrogen as products of an aqueous dissolution of sulphur oxide. In the case of the definition of a strong Brønsted-Lowry acid, only 50% got both marks, often failing to define "strong" but in other cases defining them as bases even.

Suggest why many chemicals, including hydrogen peroxide, are kept in brown bottles instead of clear colourless bottles.

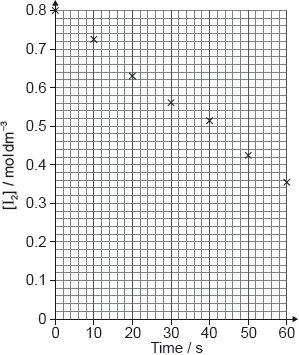
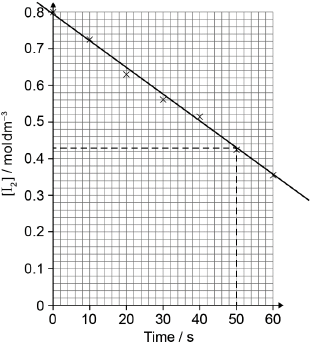
In a laboratory experiment solutions of potassium iodide and hydrogen peroxide were mixed and the volume of oxygen generated was recorded. The volume was adjusted to 0 at t = 0.

The data for the first trial is given below.

Plot a graph on the axes below and from it determine the average rate of
formation of oxygen gas in cm³ O₂ (g) s⁻¹.

Average rate of reaction:

Two more trials (2 and 3) were carried out. The results are given below.

Determine the rate equation for the reaction and its overall order, using your answer from (b)(i).

Rate equation: 

Overall order: 

Additional experiments were carried out at an elevated temperature. On the axes below, sketch Maxwell–Boltzmann energy distribution curves at two temperatures T₁ and T₂, where T₂ > T₁.

Apart from a greater frequency of collisions, explain, by annotating your graphs in (b)(iii), why an increased temperature causes the rate of reaction to increase.

MnO₂ is another possible catalyst for the reaction. State the IUPAC name for MnO₂.

Comment on why peracetic acid, CH3COOOH, is always sold in solution with ethanoic acid and hydrogen peroxide.

H₂O₂ (aq) + CH₃COOH (aq) ⇌ CH₃COOOH (aq) + H₂O (l)

Sodium percarbonate, 2Na₂CO₃•3H₂O₂, is an adduct of sodium carbonate and hydrogen peroxide and is used as a cleaning agent.

M_r (2Na₂CO₃•3H₂O₂) = 314.04

Calculate the percentage by mass of hydrogen peroxide in sodium percarbonate, giving your answer to two decimal places.

decomposes in light    [✔]

Note: Accept “sensitive to light”.

points correctly plotted     [✔]

best fit line AND extended through (to) the origin   [✔]

Average rate of reaction:
«slope (gradient) of line =» 0.022 «cm³ O₂ (g) s⁻¹»   [✔]

Note: Accept range 0.020–0.024cm³ O₂ (g) s⁻¹.

Rate equation:
Rate = k[H₂O₂] × [KI]     [✔]

Overall order:
2     [✔]

Note: Rate constant must be included.

peak of T₂ to right of AND lower than T₁     [✔]

lines begin at origin AND T₂ must finish above T₁     [✔]

E_a marked on graph    [✔]

explanation in terms of more “particles” with E ≥ E_a

OR

greater area under curve to the right of E_a in T₂     [✔]

manganese(IV) oxide

OR

manganese dioxide     [✔]

Note: Accept “manganese(IV) dioxide”.

moves «position of» equilibrium to right/products    [✔]

Note: Accept “reactants are always present as the reaction is in equilibrium”.

M( H₂O₂) «= 2 × 1.01 + 2 × 16.00» = 34.02 «g»     [✔]

«% H₂O₂ = 3 × $\frac{34.02}{314.04}$ × 100 =» 32.50 «%»     [✔]

Note: Award [2] for correct final answer.

There were a couple of comments claiming that this NOS question on “why to store hydrogen peroxide in brown bottles” is not the syllabus. Most candidates were quite capable of reasoning this out.

Most candidates could plot a best fit line and find the slope to calculate an average rate of reaction.

Good performance but with answers that either typically included only [H₂O₂] with first or second order equation or even suggesting zero order rate equation.

Fair performance; errors including not starting the two curves at the origin, drawing peak for T2 above T1, T2 finishing below T1 or curves crossing the x-axis.

The majority of candidates earned at least one mark, many both marks. Errors included not annotating the graph with E_a and referring to increase of kinetic energy as reason for higher rate at T2.

A well answered question. Very few candidates had problem with nomenclature.

One teacher suggested that “stored” would have been better than “sold” for this question. There were a lot of irrelevant answers with many believing the back reaction was an acid dissociation.

It is recommended that candidates use the relative atomic masses given in the periodic table.

State the electron configuration of the Cu⁺ ion.

Copper(II) chloride is used as a catalyst in the production of chlorine from hydrogen chloride.

4HCl (g) + O₂ (g) → 2Cl₂ (g) + 2H₂O (g)

Calculate the standard enthalpy change, ΔH^θ, in kJ, for this reaction, using section 12 of the data booklet.

The diagram shows the Maxwell–Boltzmann distribution and potential energy profile for the reaction without a catalyst.

Annotate both charts to show the activation energy for the catalysed reaction, using the label E_{a (cat)}.

Explain how the catalyst increases the rate of the reaction.

Solid copper(II) chloride absorbs moisture from the atmosphere to form a hydrate of formula CuCl₂•$x$H₂O.

A student heated a sample of hydrated copper(II) chloride, in order to determine the value of $x$. The following results were obtained:

Mass of crucible = 16.221 g
Initial mass of crucible and hydrated copper(II) chloride = 18.360 g
Final mass of crucible and anhydrous copper(II) chloride = 17.917 g

Determine the value of $x$.

State how current is conducted through the wires and through the electrolyte.

Wires: 

Electrolyte:

Write the half-equation for the formation of gas bubbles at electrode 1.

Bubbles of gas were also observed at another electrode. Identify the electrode and the gas.

Electrode number (on diagram):

Name of gas: 

Deduce the half-equation for the formation of the gas identified in (c)(iii).

Determine the enthalpy of solution of copper(II) chloride, using data from sections 18 and 20 of the data booklet.

The enthalpy of hydration of the copper(II) ion is −2161 kJ mol⁻¹.

Calculate the cell potential at 298 K for the disproportionation reaction, in V, using section 24 of the data booklet.

Comment on the spontaneity of the disproportionation reaction at 298 K.

Calculate the standard Gibbs free energy change, ΔG^θ, to two significant figures, for the disproportionation at 298 K. Use your answer from (e)(i) and sections 1 and 2 of the data booklet.

Suggest, giving a reason, whether the entropy of the system increases or decreases during the disproportionation.

Deduce, giving a reason, the sign of the standard enthalpy change, ΔH^θ, for the disproportionation reaction at 298 K.

Predict, giving a reason, the effect of increasing temperature on the stability of copper(I) chloride solution.

Describe how the blue colour is produced in the Cu(II) solution. Refer to section 17 of the data booklet.

Deduce why the Cu(I) solution is colourless.

When excess ammonia is added to copper(II) chloride solution, the dark blue complex ion, [Cu(NH₃)₄(H₂O)₂]²⁺, forms.

State the molecular geometry of this complex ion, and the bond angles within it.

Molecular geometry:

Bond angles: 

Examine the relationship between the Brønsted–Lowry and Lewis definitions of a base, referring to the ligands in the complex ion [CuCl₄]²⁻.

[Ar] 3d¹⁰
OR
1s² 2s² 2p⁶ 3s² 3p⁶ 3d¹⁰ ✔

ΔH^θ = ΣΔH^θ_f (products) − ΣΔH^θ_f (reactants) ✔
ΔH^θ = 2(−241.8 «kJ mol⁻¹») − 4(−92.3 «kJ mol⁻¹») = −114.4 «kJ» ✔

NOTE: Award [2] for correct final answer.

E_{a (cat)} to the left of E_a ✔                        

peak lower AND E_{a (cat)} smaller ✔

«catalyst provides an» alternative pathway ✔

«with» lower E_a
OR
higher proportion of/more particles with «kinetic» E ≥ E_a(cat) «than E_a» ✔

mass of H₂O = «18.360 g – 17.917 g =» 0.443 «g» AND mass of CuCl₂ = «17.917 g – 16.221 g =» 1.696 «g» ✔

moles of H₂O = «$\frac{0.443 \text{g}}{18.02 \text{g\hspace{0.05em}mo}{\text{l}}^{-1}}$=» 0.0246 «mol»
OR
moles of CuCl₂ =«$\frac{1.696 \text{g}}{134.45 \text{g\hspace{0.05em}mo}{\text{l}}^{-1}}$= » 0.0126 «mol» ✔

«water : copper(II) chloride = 1.95 : 1»

«$x$ =» 2 ✔

NOTE: Accept «$x$ =» 1.95.

NOTE: Award [3] for correct final answer.

Wires:
«delocalized» electrons «flow» ✔

Electrolyte:
«mobile» ions «flow» ✔

2Cl⁻ → Cl₂ (g) + 2e⁻
OR
Cl⁻ → $\frac{1}{2}$Cl₂ (g) + e⁻ ✔

NOTE: Accept e for e⁻.

«electrode» 3 AND oxygen/O₂ ✔

NOTE: Accept chlorine/Cl₂.

2H₂O (l) → 4H⁺ (aq) + O₂ (g) + 4e^– ✔

NOTE: Accept 2Cl^– (aq) → Cl₂ (g) + 2e^–.
Accept 4OH⁻ → 2H₂O + O₂ + 4e⁻

enthalpy of solution = lattice enthalpy + enthalpies of hydration «of Cu²⁺ and Cl⁻» ✔

«+2824 kJ mol^–1 − 2161 kJ mol^–1 − 2(359 kJ mol^–1) =» −55 «kJ mol^–1» ✔

NOTE: Accept enthalpy cycle.
Award [2] for correct final answer.

E^θ = «+0.52 – 0.15 = +» 0.37 «V» ✔

spontaneous AND E^θ positive ✔

ΔG^θ = «−nFE = −1 mol × 96 500 C Mol^–1 × 0.37 V=» −36 000 J/−36 kJ ✔

NOTE: Accept “−18 kJ mol^–1 «per mole of Cu⁺»”.

Do not accept values of n other than 1.

Apply SF in this question.

Accept J/kJ or J mol⁻¹/kJ mol⁻¹ for units.

2 mol (aq) → 1 mol (aq) AND decreases ✔

NOTE: Accept “solid formed from aqueous solution AND decreases”.
Do not accept 2 mol → 1 mol without (aq).

ΔG^θ < 0 AND ΔS^θ < 0 AND ΔH^θ < 0
OR
ΔG^θ + TΔS^θ < 0 AND ΔH^θ < 0 ✔

TΔS more negative «reducing spontaneity» AND stability increases ✔

NOTE: Accept calculation showing non-spontaneity at 433 K.

«ligands cause» d-orbitals «to» split ✔

light absorbed as electrons transit to higher energy level «in d–d transitions»
OR
light absorbed as electrons promoted ✔

energy gap corresponds to «orange» light in visible region of spectrum ✔

colour observed is complementary ✔

full «3»d sub-level/orbitals
OR
no d–d transition possible «and therefore no colour» ✔

octahedral AND 90° «180° for axial» ✔

NOTE: Accept square-based bi-pyramid.

Any two of:
ligand/chloride ion Lewis base AND donates e-pair ✔
not Brønsted–Lowry base AND does not accept proton/H⁺ ✔
Lewis definition extends/broader than Brønsted–Lowry definition ✔